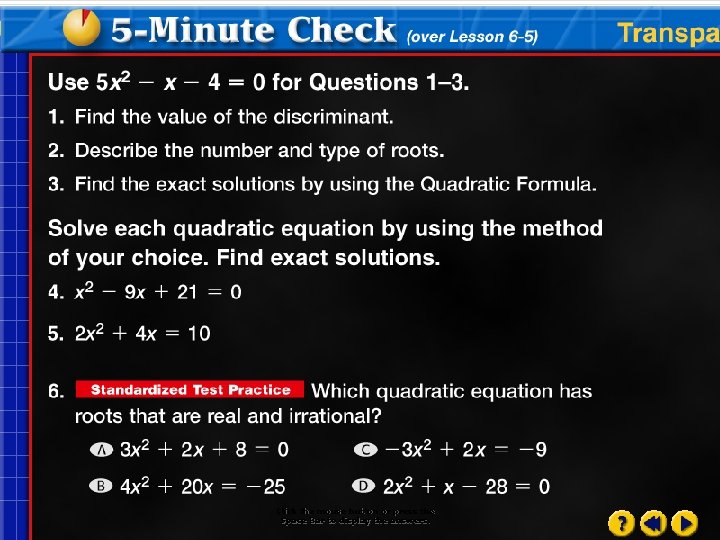
Question The Curve Below Is The Graph Of (x^2 Y^2 1)^3 x^2 Y^3 = 0 (a) Sketch The Tangent Line To To Graph At The Point (1,1) (to) Find An Equation Of Line Which Is Tangent To The Graph At The Point (11) Protip Plug In (1,1) After Applying D/dx To Both Sides Of The Equation But Before Solving For Dy/dt Ex 21, 1 If (x/3 " 1, y –" 2/3) = (5/3 "," 1/3) , find the values of x and y (x/3 " 1, y –" 2/3) = (5/3 "," 1/3) Since the ordered pairs are equal, corresponding elements are equal Hence x/3 1 = 5/3 x/3 = 5/3 – 1 x/3 = 2/3 x = 2 y – 2/3 = 1/3Click here👆to get an answer to your question ️ If x,y,z are all different and if x & x^2 & 1 x^3 y & y^2 & 1 y^3 z & z^2 & 1 z^3 = 0 then 1 xyz =

Warmup 1 Solve By Factoring 2 Write The
(x^2 y^2-1)^3-x^2*y^3=0 significato
(x^2 y^2-1)^3-x^2*y^3=0 significato-Circle on a Graph Let us put a circle of radius 5 on a graph Now let's work out exactly where all the points are We make a rightangled triangle And then use Pythagoras x 2 y 2 = 5 2 There are an infinite number of those points, here are some examples11 Find roots (zeroes) of F(x) = x 3 x 22 Polynomial Roots Calculator is a set of methods aimed at finding values of x for which F(x)=0 Rational Roots Test is one of the above mentioned tools It would only find Rational Roots that is numbers x which can be expressed as the quotient of two integers The Rational
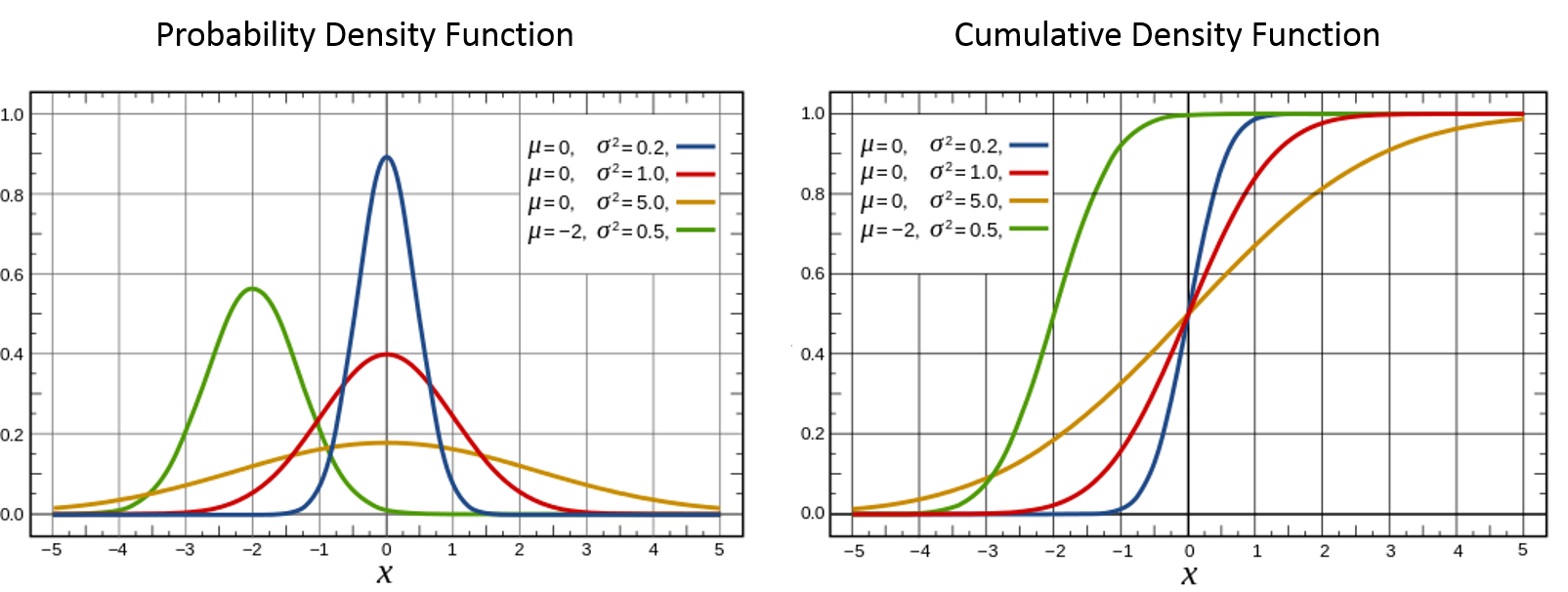



Sampling From A Normal Distribution Bounded Rationality
Do y=2 to 2 by 001;Dx = " 3x2 2 − x3 2 # 1 x=0 = 1 Note that Methods 1 and 2 give the same answer If they don't it means something is wrong 011 Example Evaluate ZZ D (4x2)dA where D is the region enclosed by the curves y = x2 and y = 2x Solution Again we will carry out the integration both ways, x first then ySimple and best practice solution for x(y^2)x3(y^2)1=0 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homework
I need to draw (pencil and paper) the region bounded by x 2 y 2 = 1, y = z, x = 0, and z = 0 in the first octant So the first assistance I asked of Mathematica is I was then able to draw the image via pencil and paper Then I thought I'd try RegionFunction ContourPlot3D {x^2 y^2 == 1, y == z, x == 0, z == 0}, {x, 0, 1}, {y, 0, 1}, {zOrdinary Differential Equations 1 Introduction A differential equation is an equation relating an independent variable, eg t, a dependent variable, y, and one or more derivatives of y with respect to t dx dt = 3x y2 dy dt = et d2y dx2 3x2y2 dy dx = 0Plotting X 2 Y 2 1 3 X 2 Y 3 0 Mathematics Stack Exchange For more information and source, see on this link https//mathstackexchangecom/questions/
1 Answer1 Active Oldest Votes 3 The solution set is obviously symmetric with respect to the y axis Therefore we may assume x ≥ 0 In the domain { ( x, y) ∈ R 2 x ≥ 0 } the equation is equivalent with x 2 y 2 − 1 = x 2 / 3 y , which can easily be solved for y y = 1 2 ( x 2 / 3 ± x 4 / 3 4 ( 1 − x 2Y 2 y 2 • x 2 y 2 = —— = ——————— 1 x 2 Equivalent fraction The fraction thus generated looks different but has the same value as the whole Common denominator The equivalent fraction and the other fraction involved in the calculation share the same denominator Adding fractions that have a common denominatorThe intersection of the two graphs is ( 2;




24 Y X2 3 X2 Y2 5 A X 2 Y 1 X 1 Y 2 X Chegg Com




Y X 3 Y 0 X 2 Novocom Top
Free Online Scientific Notation Calculator Solve advanced problems in Physics, Mathematics and Engineering Math Expression Renderer, Plots, Unit Converter, Equation Solver, Complex Numbers, Calculation HistoryUnlock StepbyStep (x^2y^21)^3x^2y^3=0 Extended Keyboard Examples * Generate x,y pairs to closely fit Valentine equation (x**2y**21)**3x**2*y**3=0;




Warmup 1 Solve By Factoring 2 Write The



Solutions College Algebra
Subject to the constraint 2x2 (y 1)2 18 Solution We check for the critical points in the interior f x = 2x;f y = 2(y1) =)(0;Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and morePlotting X 2 Y 2 1 3 X 2 Y 3 0 Mathematics Stack Exchange For more information and source, see on this link https Solved The Curve Below Is The Graph Of X 2 Y 2 1 3 X Chegg Com For more information and source, see on this link https




Y X 3 Y 0 X 2 Novocom Top



2
3x−x2 − x2 2!(x;0) with 0 x 2 Call this set B 2 The nal side of the triangle is the line segment from (2;0) to (0;Review for Exam 3 I Tuesday Recitations 147, , half 157 I Thursday Recitations , 157 I 50 minutes I From five 10minute problems to ten 5minutes problems I Problems similar to homework problems I No calculators, no notes, no books, no phones Double integrals in Cartesian coordinates (Section 152) Example Switch the integration order in I =




Tutto 1 Di 2 Flashcards Quizlet



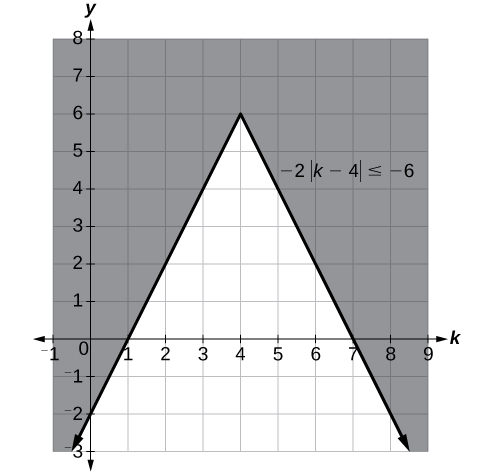
Absolute Value Inequalities
Solve by Factoring x^(2/3)3x^(1/3)10=0 Rewrite as Let Substitute for all occurrences of Factor using the AC method Tap for more steps Consider the form Find a pair of integers whose product is and whose sum is In this case, whose product is and whose sum isP(X2 Y2 > 1) = 1− π/24 Well, instead of this complicated (but straightforward) solution we can look at the geometry instead because here the density is uniform The area of interest is {(x,y) x2 y2 > 1,0 < x < 2,0 < y < 3} Draw it and see that the area is 6 − π/4 Then multiply the area by 1/6 and get the answer 9 Problem 391Simple and best practice solution for 2(y2)(x3)(1y)=0 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homework




Nth Root Wikipedia
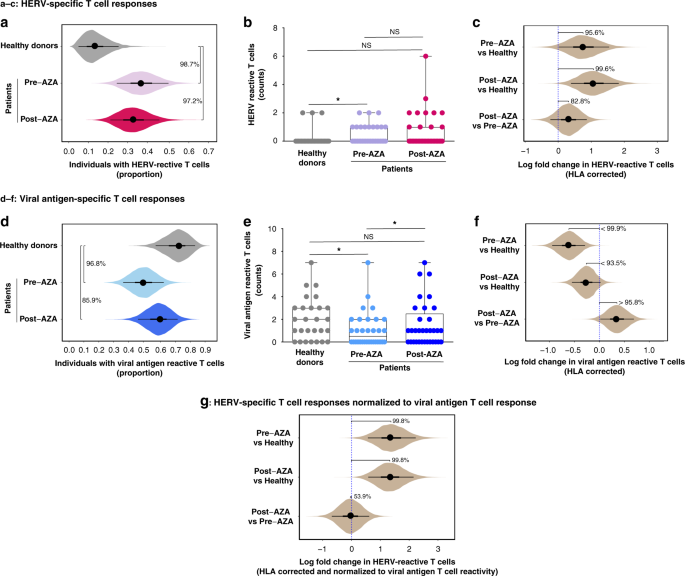



Human Endogenous Retroviruses Form A Reservoir Of T Cell Targets In Hematological Cancers Nature Communications
1) is a critical point The second derivative test f xx = 2;f yy = 2;f xy = 0 shows this a local minimum withSis the surface of the solid bounded by the paraboloid z= 1 x2 y2 and the xyplane ZZ S FdS= ZZZ E div FdV div F= 6x 2 3y2 3y = 6(x2 y2) ZZZ E 6(x2 y2) dV = 6 Z 2ˇ 0 Z 1 0 Z 1 r2 0 r2rdzdrd = 6 Z 2ˇ 0 Z 1 0 r3 z 1 2r 0 drd = 6Partial Differential Equations Exam 1 Review Solutions Spring 18 Exercise 1 Verify that both u= log(x2y2) and u= arctan(y=x) are solutions of Laplace's equation u xx u yy= 0 If u= log(x2 y2), then by the chain rule u x= 2x x 2 y) u xx= (x2 y2)(2) (2x)(2x) (x 2 y) 2y2 2x2 (x y2)2 and by the symmetry of uin xand y,




Saddle Point Wikipedia




2 Associative Analysis
1) The line through these two points has slope 1=2, and can thus be written as y = x=2 1 That is, the last subset of the boundary, B 3, is the set of points (x;x=2 1) with 0 x 2Find the volume V of the solid bounded by the cylinder $x^2 y^2 = 1$, the xyplane and the plane $x z = 1 $ Hi all, i cant seem to get the correct answer for thisSubtracting x 2 from itself leaves 0 \left (yx^ {\frac {2} {3}}\right)^ {2}=1x^ {2} ( y − x 3 2 ) 2 = 1 − x 2 Take the square root of both sides of the equation Take the square root of both sides of the equation yx^ {\frac {2} {3}}=\sqrt {1x^ {2}} yx^ {\frac {2} {3}}=\sqrt {1x^ {2}}




Chapter 9 Computation Of Discrete Fourier Transform



Iqmol Symmol F90 At Master Nutjunkie Iqmol Github
Do x=2 to 2 by 001;Z 1−x/2−z/3 0 dy dz dx V = Z 3 0 Z 2−2z/3 0 Z 1−x/2−z/3 0 dy dx dz C Triple integrals in Cartesian coordinates (Sect 154) I Review Triple integrals in arbitrary domains I Examples Changing the order of integration I The average value of a function in a region in space(x^2 y^21)^3 x^2y^3 = 0 WolframAlpha April 21 Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals




Pdf The Lambert Function The Quintic Equation And The Proactive Discovery Of The Implicit Function Theorem
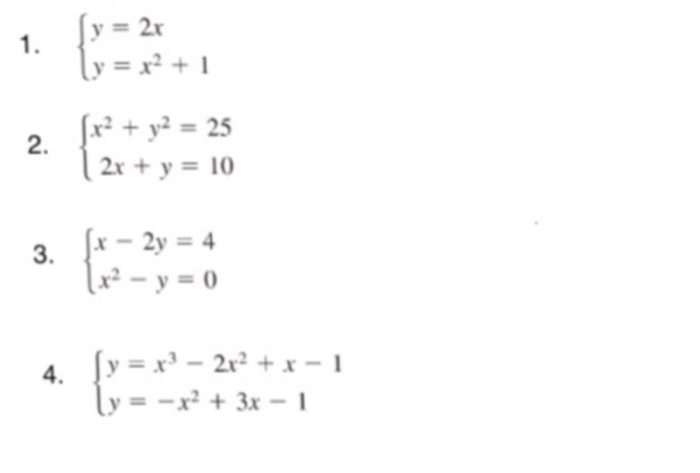



Y 2x 1 X2 1 2 La X2 Y2 25 2x Y 10 X 2y 4 Chegg Com
If x, y, z are different and Δ = (x, x2, 1 x3), (y, y2, 1 y3), (z, z2, 1 z3) = 0 then show that 1 xyz = 0 We have Now, we know that If some or all elements of a row or column of a determinant are expressed as sum of two (or more) terms, then the determinant can be expressed as sum of two (or more) determinants Explanation In order for this limit to exist, the fraction x2 x2 y2 must approach the same value L regardless of the path along which we approach (0,0) Consider approaching (0,0) along the xaxis That means fixing y = 0 and finding the limit lim x→0 x2 x2 y2 lim x→0, y=0 x2 x2 y2 = lim x→0 x2 x2 0 = 0 0 Example 18 Solve the following pair of equations by reducing them to a pair of linear equations 5/(𝑥 −1) 1/(𝑦 −2) = 2 6/(𝑥 −1) – 3/(𝑦 −2) = 1 5/(𝑥 − 1) 1/(𝑦 − 2) = 2 6/(𝑥 − 1) – 3/(𝑦 − 2) = 1 So, our equations become 5u v = 2 6u – 3v = 1 Thus, our




A Multi Criteria Approach For Selecting The Seismic Retrofit Intervention For An Existing Structure Accounting For Expected Losses And Tax Incentives In Italy Sciencedirect
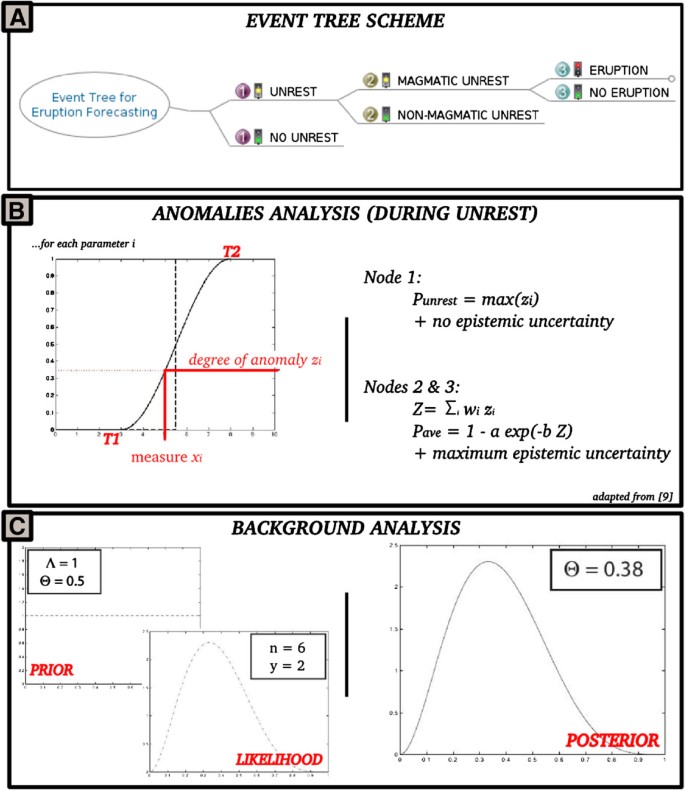



Operational Eruption Forecasting At High Risk Volcanoes The Case Of Campi Flegrei Naples Journal Of Applied Volcanology Full Text
The points (x,y,z) of the sphere x 2 y 2 z 2 = 1, satisfying the condition x = 05, are a circle y 2 z 2 = 075 of radius on the plane x = 05 The inequality y ≤ 075 holds on an arc The length of the arc is 5/6 of the length of the circle, which is why the conditional probability is equal to 5/6I have that on a shirt D The front is "I ((x 2 y 2 1) 3 x 2 y 3 < 0) Henry Sibley math team, and the back is a graph of itAnswer to Find the slope of the tangent line to the curve (x^2 y^2 1)^3 x^2 y^3 = 0 at the point (1, 1) By signing up, you'll get for Teachers for Schools for Working Scholars® for



1




Income Inequality Measures Dagum Major Reference Works Wiley Online Library
Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us! Click here 👆 to get an answer to your question ️ if x=2√3, find the value of x²1/x² baby43 baby43 Math Secondary School answered • expert verified If x=2√3, find the value of x²1/x² 2 See answers Brainly User Brainly User1) So the solution to the system of simultaneous equations is x = 2 and y = 1 We can also check the solution using algebraic methods Substitute equation ( 1) into ( 2) x = 2 y ∴ y = 2 ( 2 y) − 3 Then solve for y y − 4 y = − 3 − 3 y = − 3 ∴ y = 1




Associations Of Fats And Carbohydrate Intake With Cardiovascular Disease And Mortality In 18 Countries From Five Continents Pure A Prospective Cohort Study The Lancet



Http Docs Neu Edu Tr Staff Fahreddin Sadikoglu 3 2 Pdf
Explanation Sort the x terms and y terms x2 −x y2 2y = −1 Now, complete the square for each variable x2 −x 1 4 y2 2y 1 = −1 1 4 1 Don't forget to balance both sides of the equation (If you add something to one side, add it to the other side as well) (x − 1 2)2 (y 1)2 = 1 4 This is in the standard form of a circle(a) Z 1 0 Z x 0 f(x,y)dydx (b) Z 1 0 Z 1 x3 f(x,y)dydx 15 Calculate the double integral below by first changing the order of integration Z 1 0 Z p 3 1x2 0 p 1y3 dydx FQ FQ 16 Express the double integral below as an equivalent double integral with the order of integraDx = Z 1 0 3x− 3x2 2!
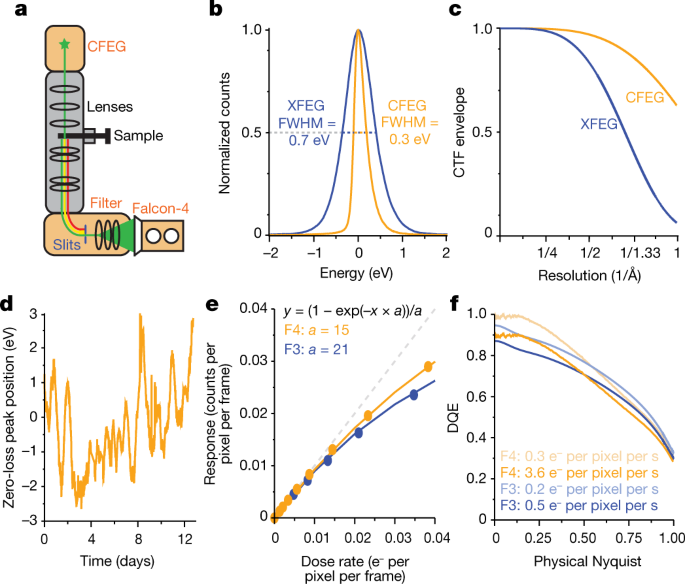



Single Particle Cryo Em At Atomic Resolution Nature




Functional Mock Up Interface Specification
There are no positive integer solutions to the diophantine equation x 2 y 2 = 1 Proof (Proof by Contradiction) Assume to the contrary that there is a solution (x, y) where x and y are positive integers If this is the case, we can factor the left side x 2 y 2 = (xy)(xy) = 1 Since x and y are integers, it follows that either xy = 1We want to set m so that for a point math(x,y)/math, the derivative math\frac{dy}{dx}/math is the same for the two curves To find the point where the two curves are the same we combine the two equations mathy = mx 1 /mathand mathxX 2 Y 2 1 3 X 2y 3 0 Wolfram Alpha Clip N Share For more information and source, see on this link https//wwwwolframalphacom/share/clip?f




X 2 Y 2 1 3 X 2 Y 3 0 Significato Novocom Top



How To Solve Math X 2 Xy Frac Y 2 3 25 Math Math Frac Y 2 3 Z 2 9 Math Math Z 2 Zx X 2 16 Math Find Math Xy 2yz 3xz Math Quora
EC02 Spring 06 HW5 Solutions 3 Problem 321 • The random variable X has probability density function fX (x) = ˆ cx 0 ≤ x ≤ 2, 0 otherwise If x^2 xy y^3 = 1, find the value of y" at the point where x = 1 Boost your resume with certification as an expert in up to 15 unique STEM subjects this summerIf the area of the circle 4 x 2 4 y 2 8 x − 1 6 y λ = 0 is 9 π sq units, then the value of λ is View solution If s , s 1 , s 2 be the circles of radii 5,3,2 respectivelyIf s 1 a n d s 2 touch externally and they touch internally with S



Differences And Approximate Derivatives Matlab Diff



Similarity Analysis Between Species Of The Genus Quercus L Fagaceae In Southern Italy Based On The Fractal Dimension
Find the volume under the paraboloid z = 4(x2) 2y 2 over the region bounded by the circles (x1) 2 y 2 = 1 and (x2) 2 y 2 = 4 Solution At first glance, this seems like a very hard volume to compute as the region R (shown in Figure 1433 (a)) has a hole in it, cutting out a strange portion of the surface, as shown in part (b) of the figureFind the area bounded by the curve y = x2x4, the xaxis and the ordinates x = 1 and x = 3 Solution If we set y = 0 we obtain the quadratic equation x 2 x 4 = 0, and for this quadratic Q331 In Exercises 331 335 use the RungeKutta method to find approximate values of the solution of the given initial value problem at the points xi = x0 ih, where x0 is the point where the initial condition is imposed and i = 1, 2 1 y ′ = 2x2 3y2 − 2, y(2) = 1;



1
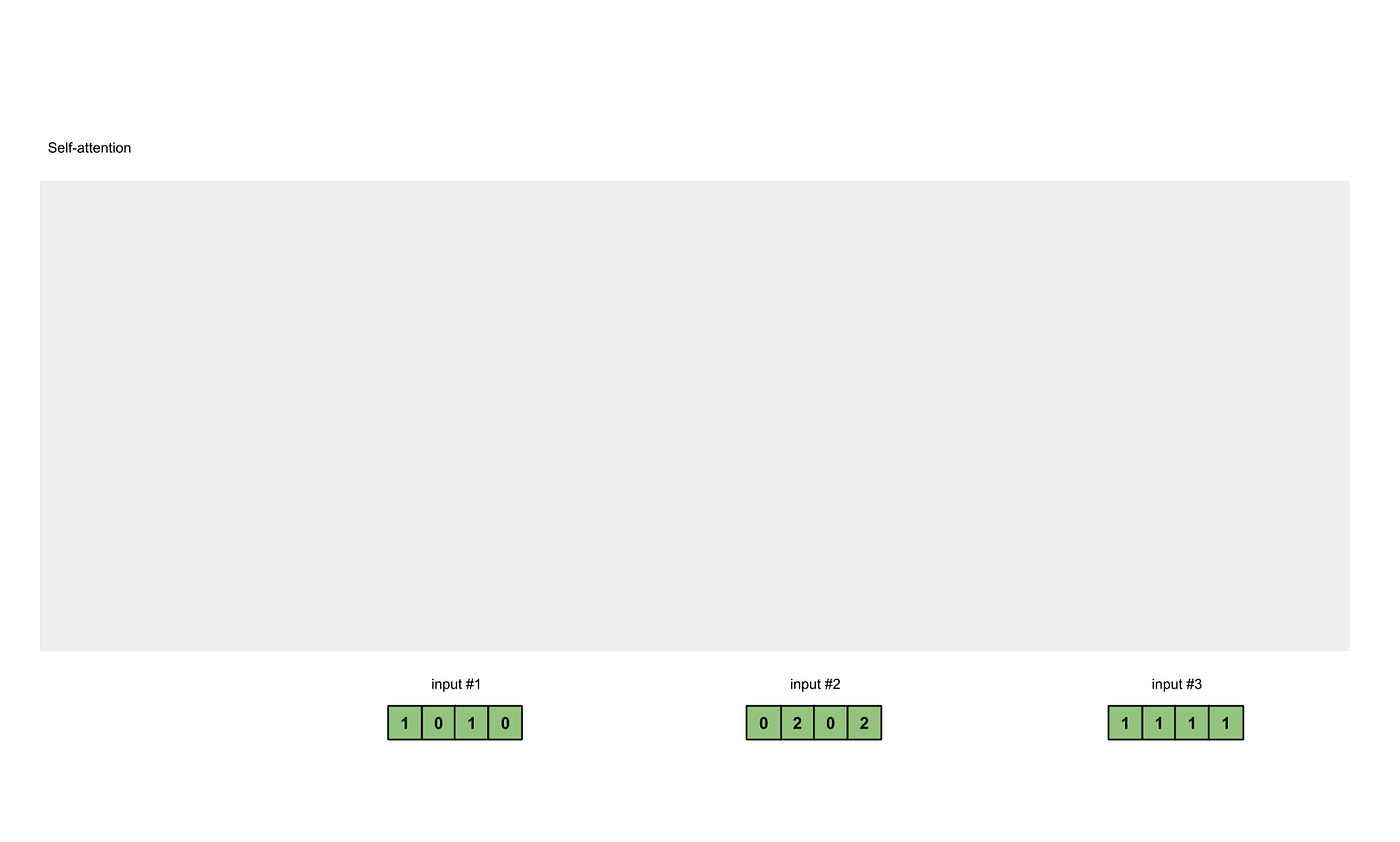



Illustrated Self Attention Step By Step Guide To Self Attention By Raimi Karim Towards Data Science




Pronounced Increase In Slope Instability Linked To Global Warming A Case Study From The Eastern European Alps Savi 21 Earth Surface Processes And Landforms Wiley Online Library




What Is A Function








Pdf The Lambert Function The Quintic Equation And The Proactive Discovery Of The Implicit Function Theorem




The Astonishing Oblivion Of Peano S




Tutto 1 Di 2 Flashcards Quizlet




Late Cenozoic Uplift Of Southern Italy Deduced From Fluvial And Marine Sediments Coupling Between Surface Processes And Lower Crustal Flow Sciencedirect



1 Solve X2 Y2 25 2x Y 10 2 Solve 2x2 Chegg Com




Tutto 1 Di 2 Flashcards Quizlet



Www Mathunion Org Fileadmin Icm Proceedings Icm1954 2 Icm1954 2 Ocr Pdf




X 2 Y 2x 2 Y 2 4xy Y 1 1 Xyy 3x 2 Chegg Com
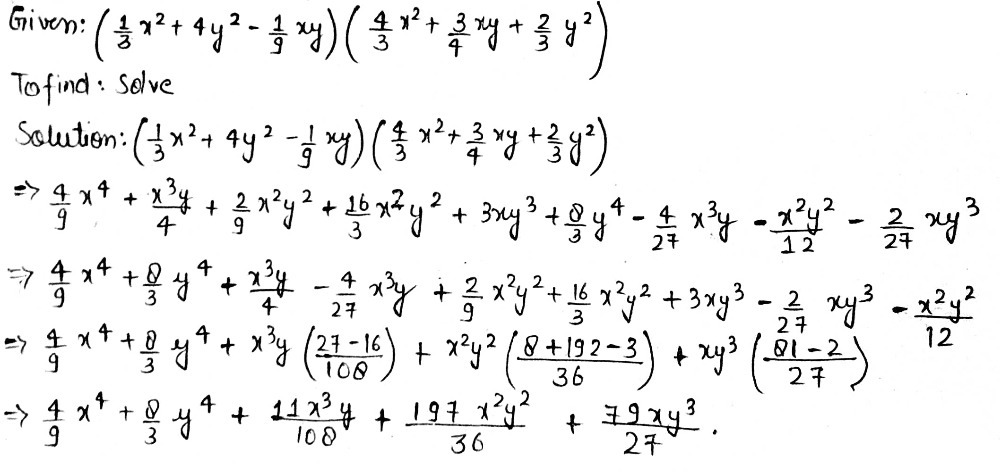



C 1 3 X2 4y2 1 9 Xy 4 3 X2 3 4 Xy 2 3 Y2 Gauthmath




Week 3 Solve Simultaneously 2y 3x 1 9x2 4y2 9x 4y 1 Ppt Download



1 Solve X2 Y2 25 2x Y 10 2 Solve 2x2 Chegg Com




Warmup 1 Solve By Factoring 2 Write The




Warmup 1 Solve By Factoring 2 Write The




Y X 3 Y 0 X 2 Novocom Top




Nth Root Wikipedia




Pdf The Lambert Function The Quintic Equation And The Proactive Discovery Of The Implicit Function Theorem




Hw8mk Wired Alarm Manualzz




X 2 Y 2 1 3 X 2 Y 3 0 Significato Novocom Top



How To Solve Math X 2 Xy Frac Y 2 3 25 Math Math Frac Y 2 3 Z 2 9 Math Math Z 2 Zx X 2 16 Math Find Math Xy 2yz 3xz Math Quora




Associations Of Fats And Carbohydrate Intake With Cardiovascular Disease And Mortality In 18 Countries From Five Continents Pure A Prospective Cohort Study The Lancet




Y X 3 Y 0 X 2 Novocom Top




Warmup 1 Solve By Factoring 2 Write The




Y X 3 Y 0 X 2 Novocom Top



Warmup 1 Solve By Factoring 2 Write The



Warmup 1 Solve By Factoring 2 Write The



H 2 0 High Resolution Stock Photography And Images Page 15 Alamy



Solutions College Algebra




Casio Ctk00 3000 Lk2 Apend All Web Ctk00 Appendix




Tutto 1 Di 2 Flashcards Quizlet




Y X 3 Y 0 X 2 Novocom Top




X 2 Y 2 1 3 X 2 Y 3 0 Significato Novocom Top



Chapter 12 Conic Sections 12 1 Parabola Distance



Geometrical Aspects Of Possibility Measures On Finite Domain Mv Clans Springerlink



Http Www Liceoscientificocarducci It Documenti 2 Sistemilineari Pdf



Inverse Function




Solve X 2 5x 6 0 Youtube



Inverse Function




Functional Mock Up Interface Specification




Solve The Following Differential Equations Y X Y 1 Y 1 2 Y X Y 1 X 2 L Y 2 X Y 2 0 Y




Revista Archivos De Filosofia N 2 Y 3 Pag 1 250 By Umce Issuu
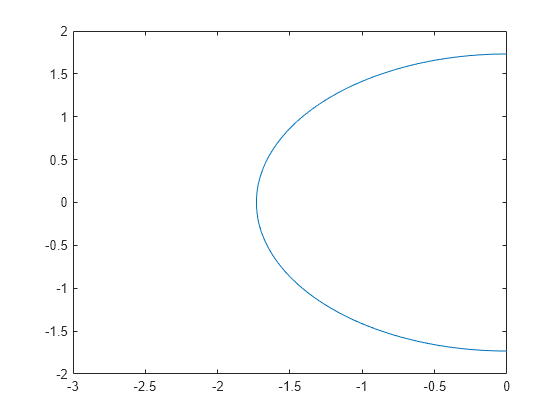



Plot Implicit Function Matlab Fimplicit



H 2 0 High Resolution Stock Photography And Images Page 15 Alamy



1



Www Mdpi Com 73 4433 12 2 6 Pdf




Sampling From A Normal Distribution Bounded Rationality




1 Solve X2 Y2 25 2x Y 10 2 Solve 2x2 Chegg Com




X 2 Y 2 1 3 X 2 Y 3 0 Novocom Top
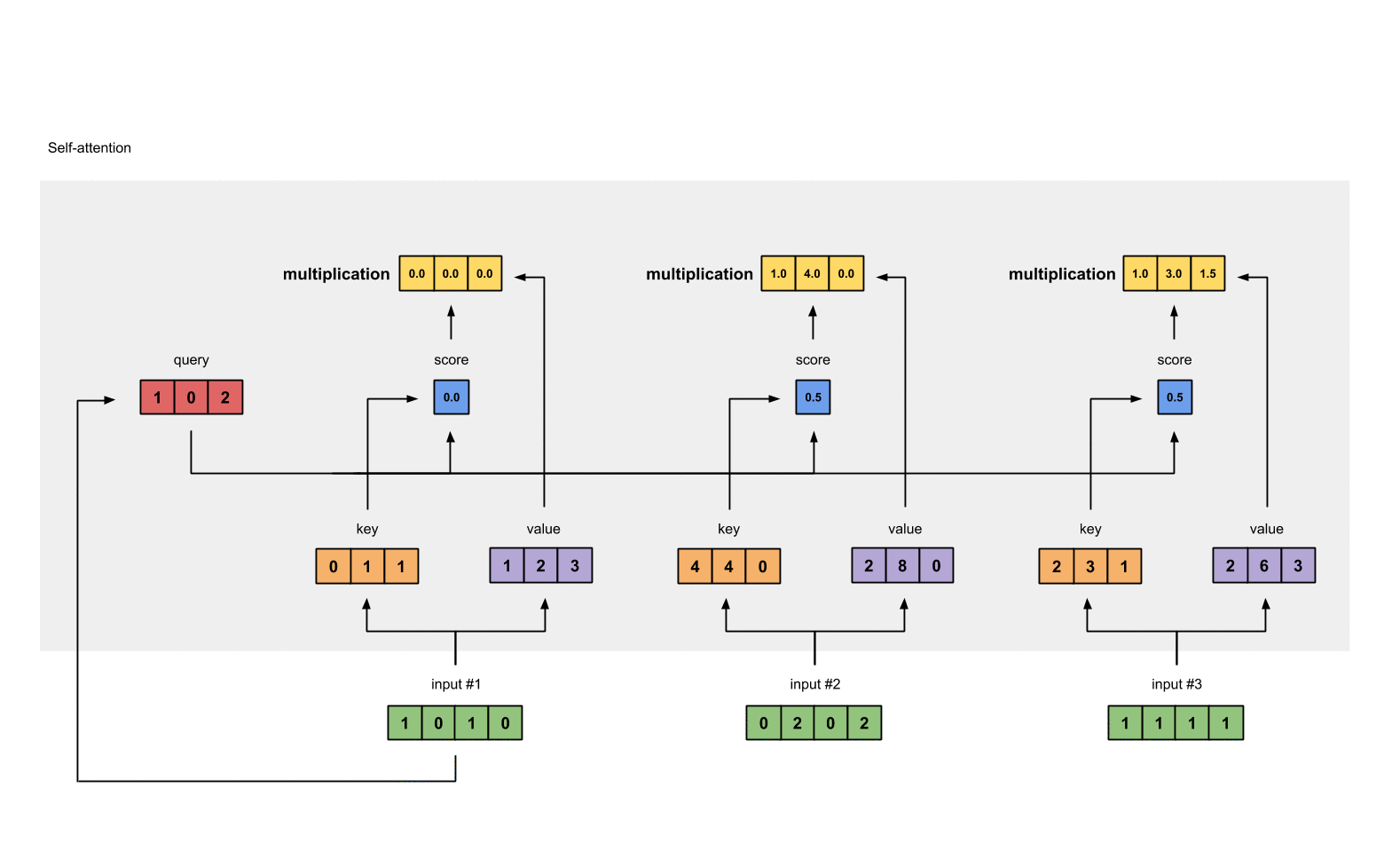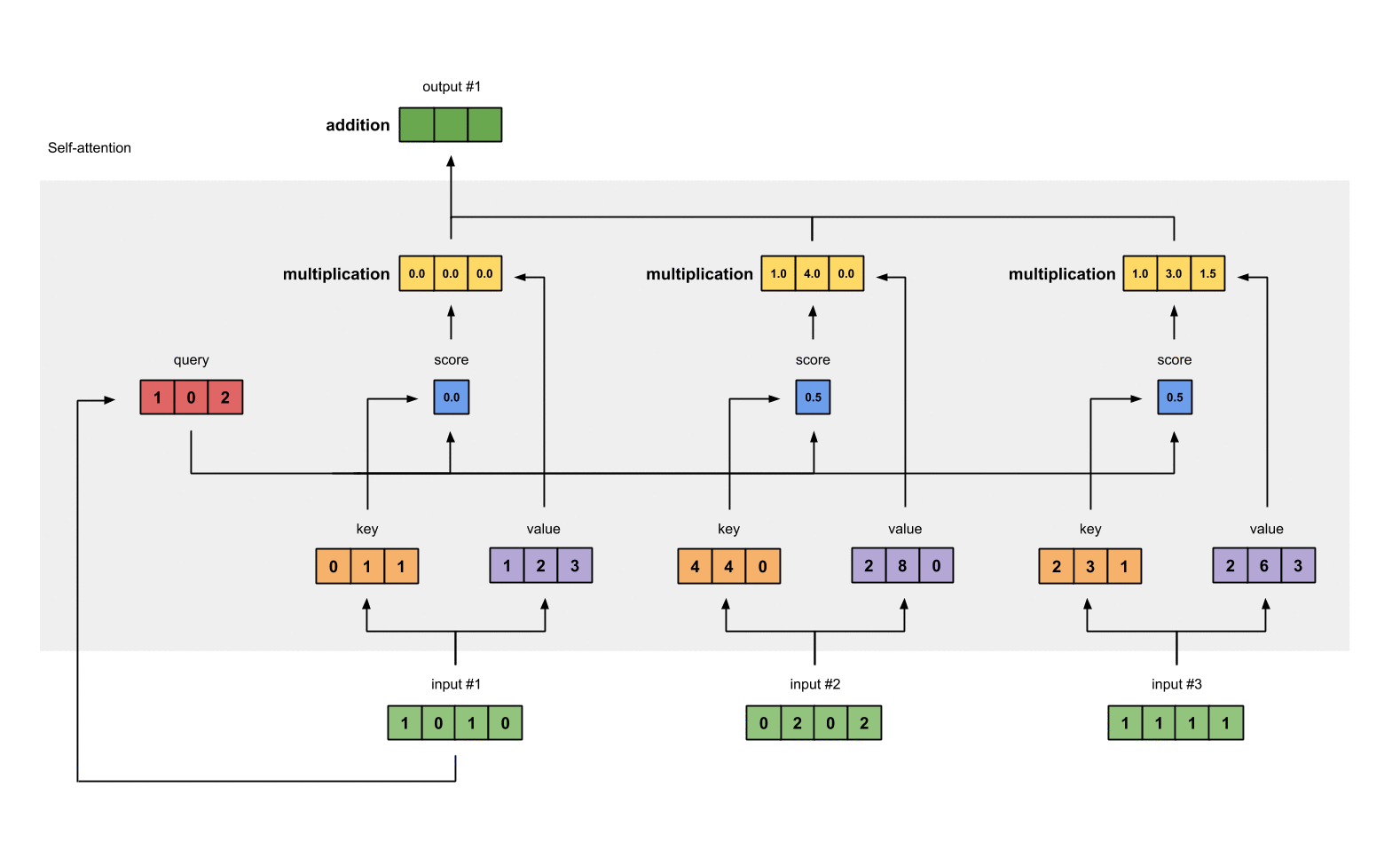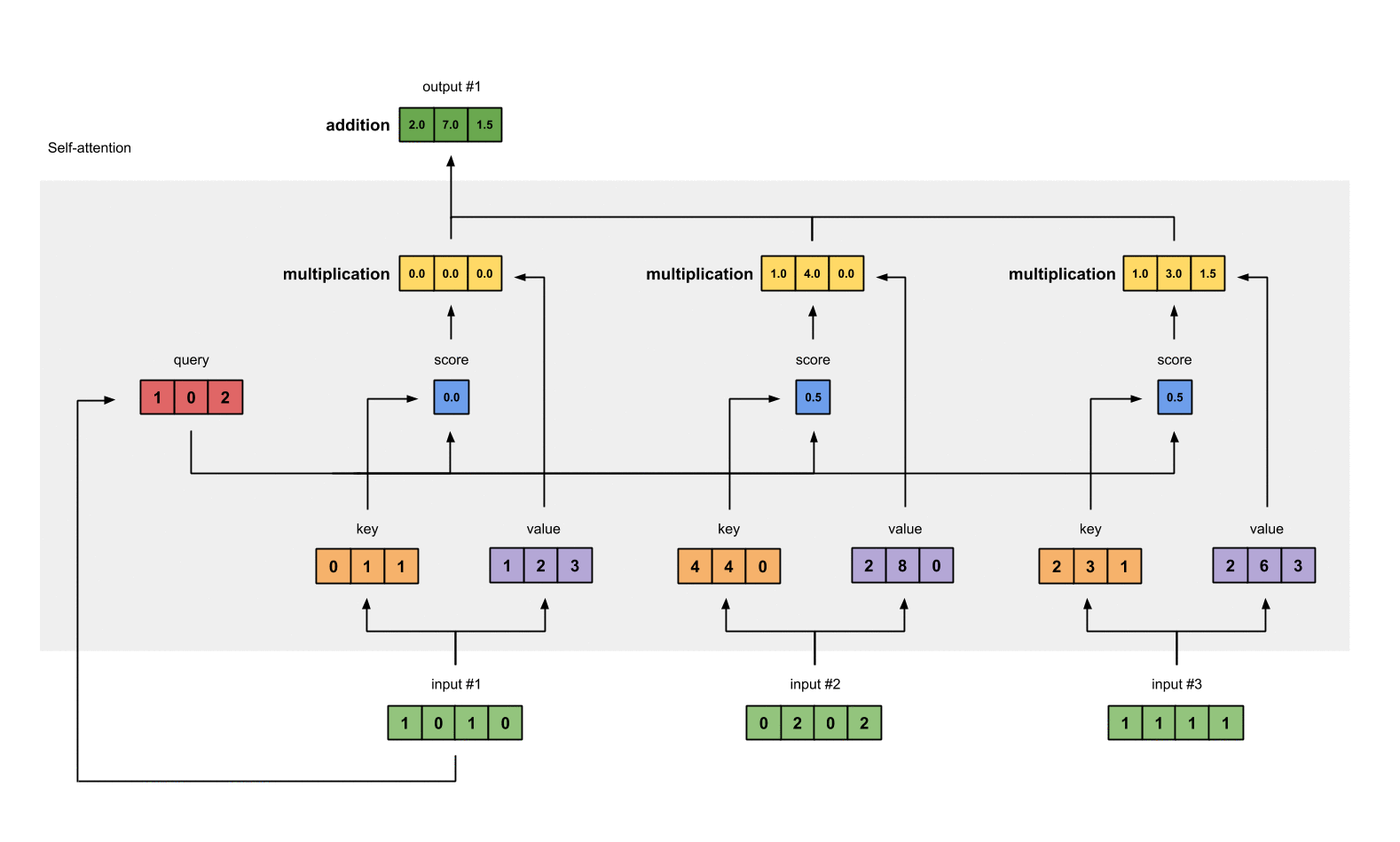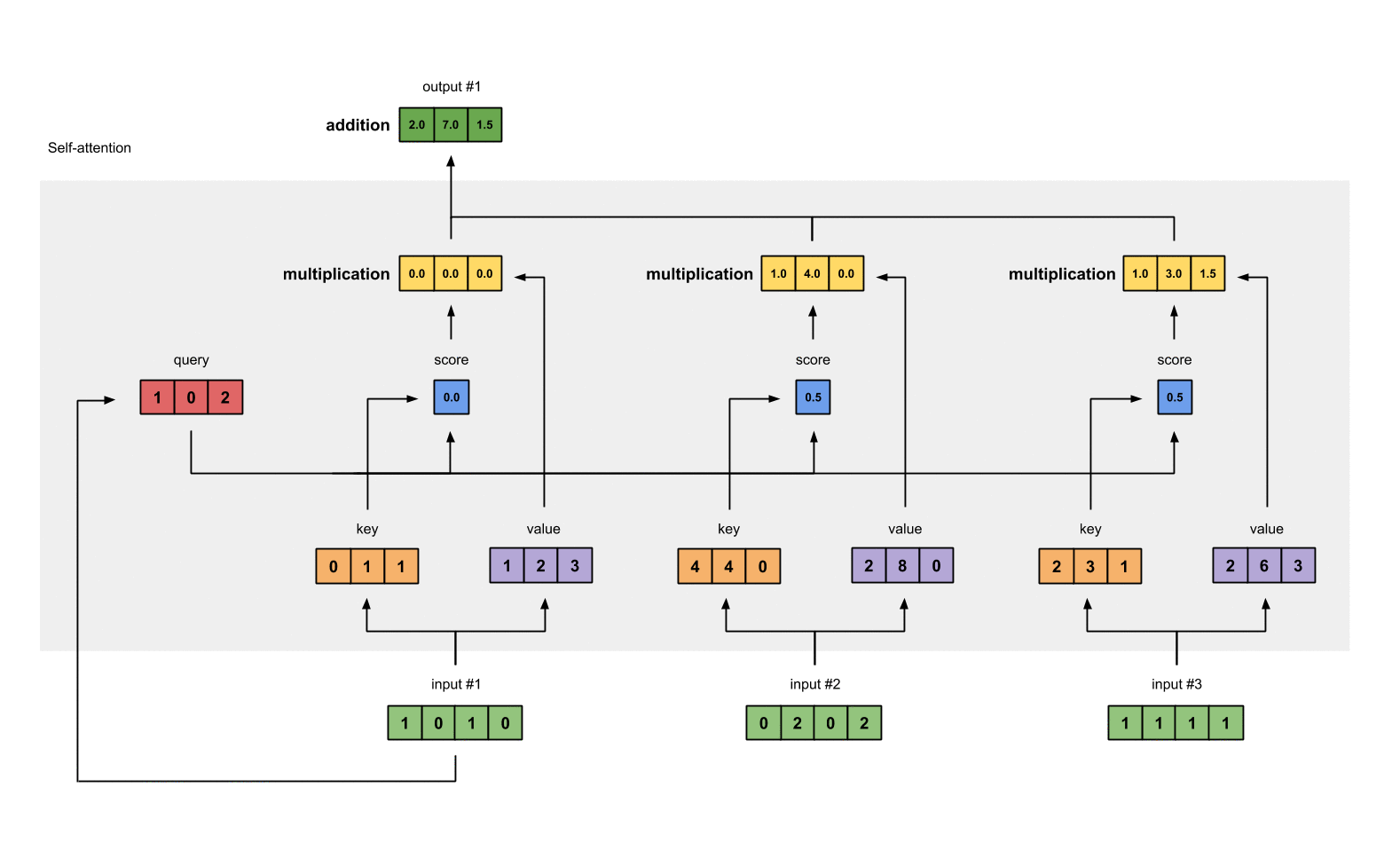



Illustrated Self Attention Step By Step Guide To Self Attention By Raimi Karim Towards Data Science
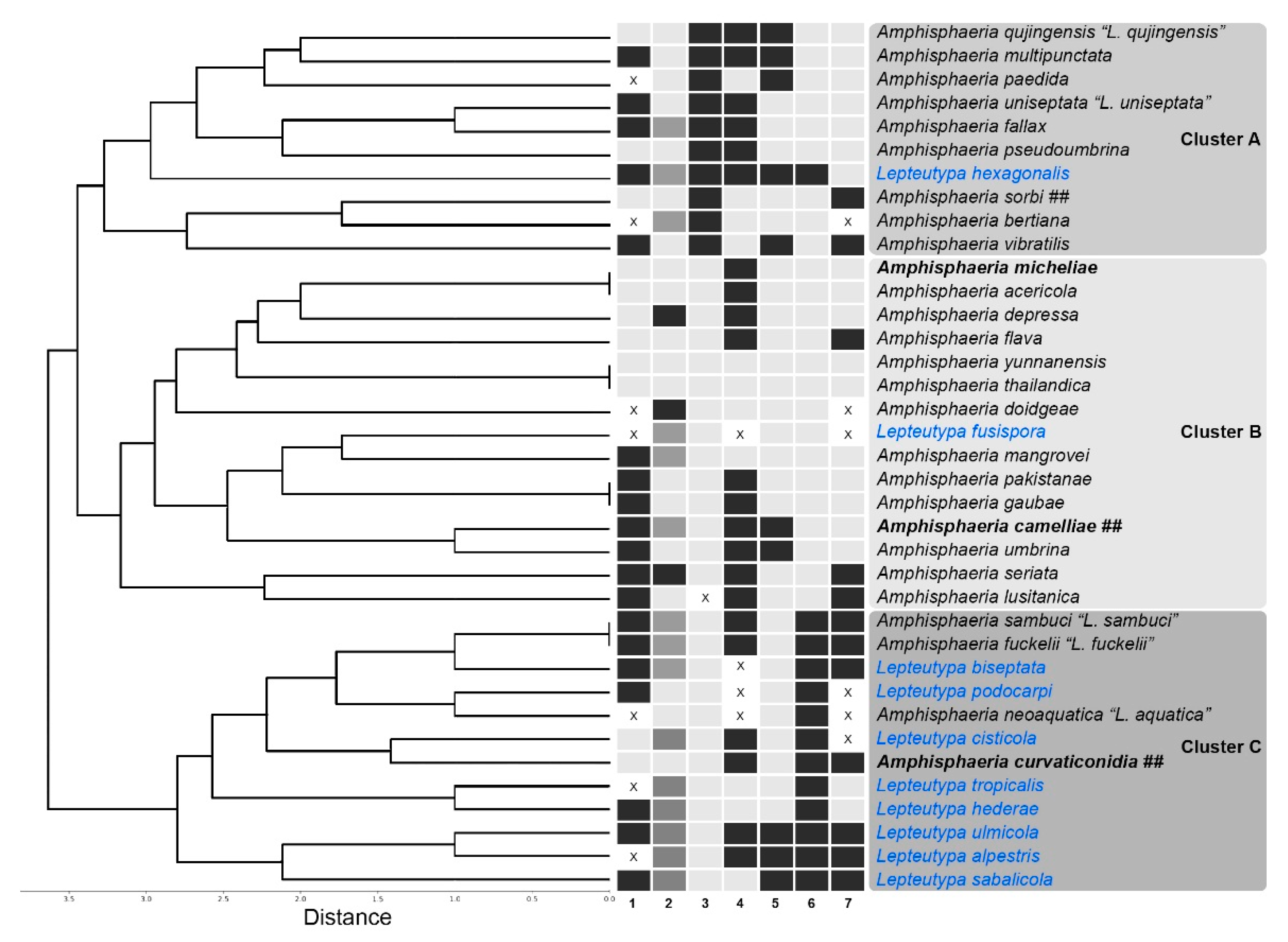



Jof Free Full Text Molecular Phylogeny And Morphology Of Amphisphaeria Lepteutypa Amphisphaeriaceae Html




Tutto 1 Di 2 Flashcards Quizlet
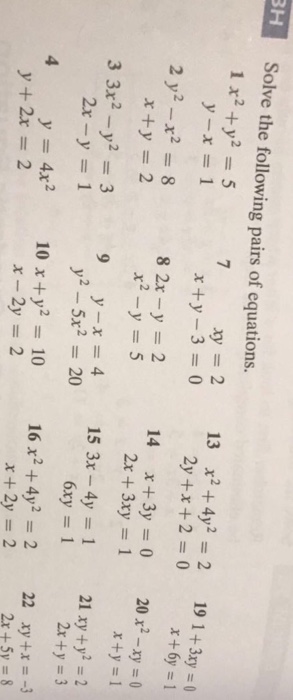



Solve The Following Pairs Of Equations 1x2 Y2 5 Chegg Com




Linear Subspace Wikipedia




On Board Systems Modeling And Power Flow Analysis For Light Rail Vehicles Design Pdf Free Download




Y X 3 Y 0 X 2 Novocom Top



Static Weg Net Medias Downloadcenter H1a H70 Weg W22 Three Phase Induction Motor Technical African Market Brochure English Web Pdf




Pdf The Lambert Function The Quintic Equation And The Proactive Discovery Of The Implicit Function Theorem



Inspirehep Net Files 5470a4a100d507fdb9e27ee8




Interface Mechanical Problems In Heterogeneous Materials
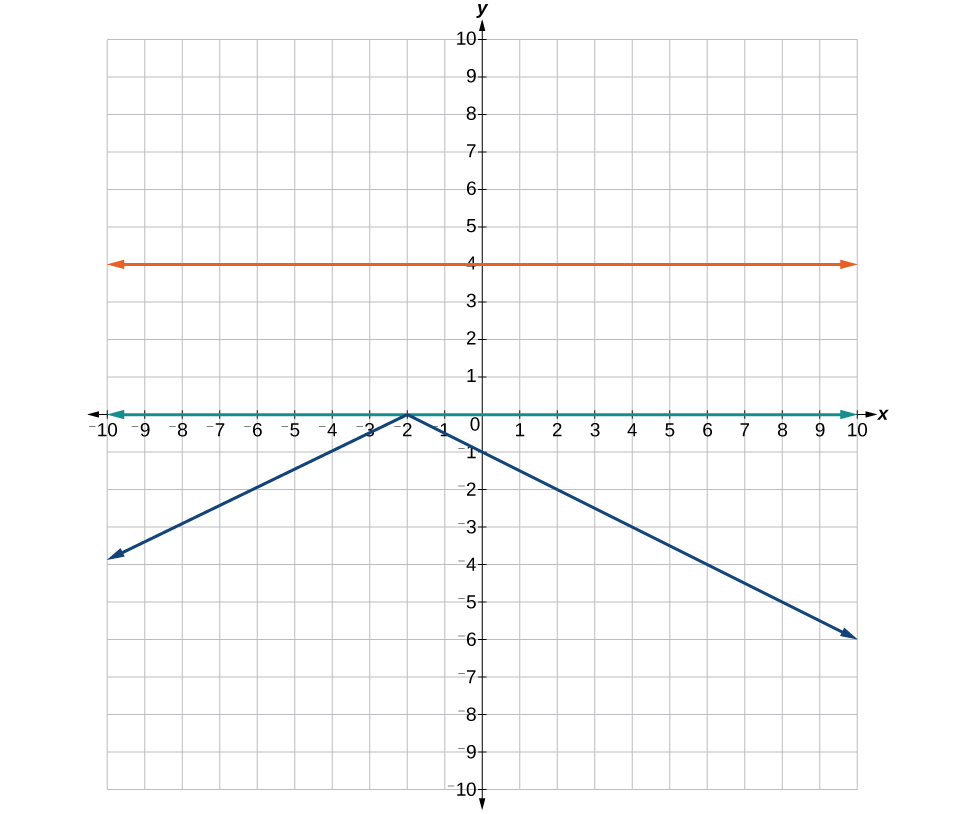



Solutions College Algebra




6amg2mfatxlbam
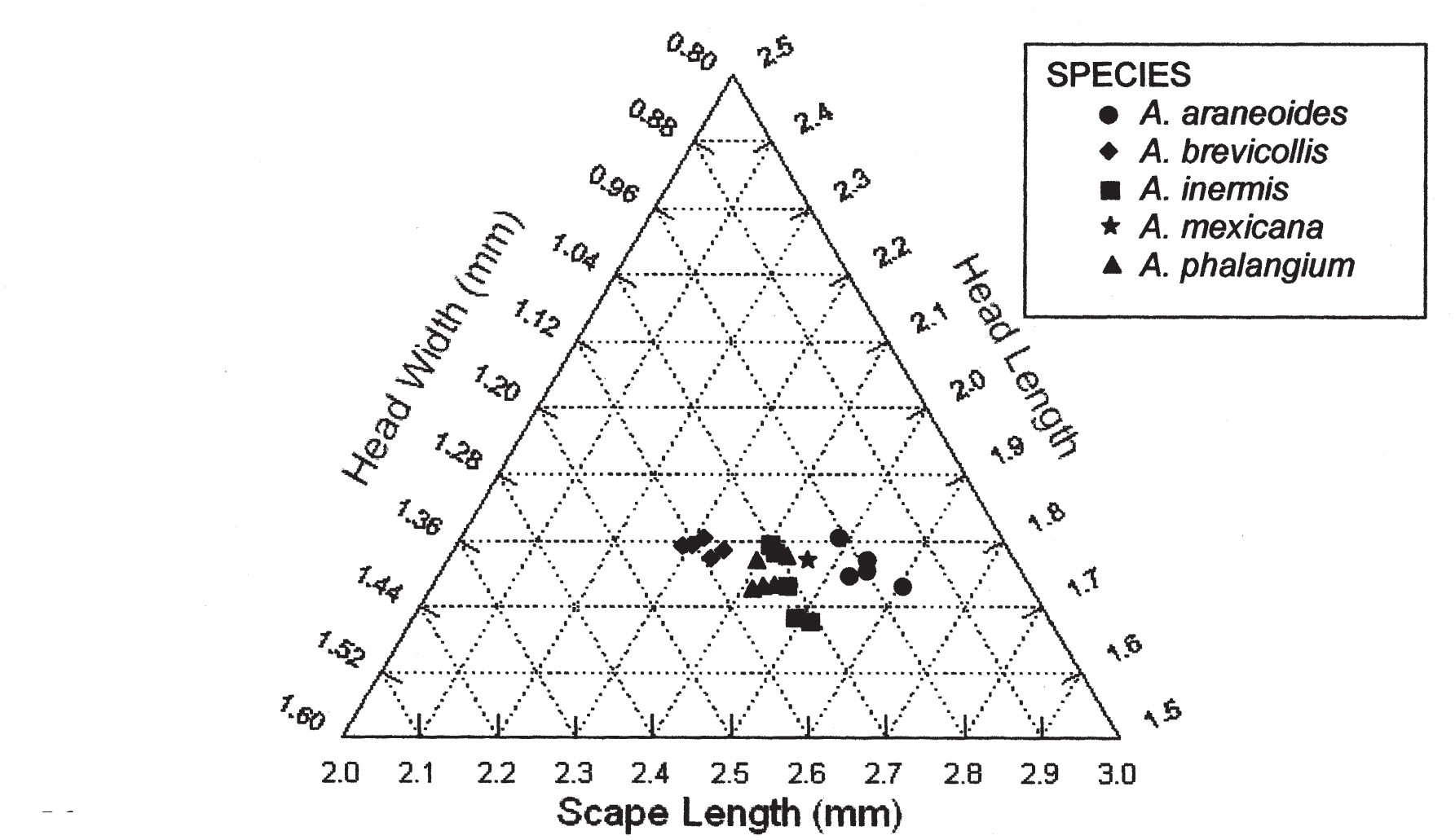



A Revision Of The Phalangium Species Complex Of The Ant Genus Aphaenogaster Hymenoptera Formicidae Myrmicinae




Plotting X 2 Y 2 1 3 X 2 Y 3 0 Mathematics Stack Exchange
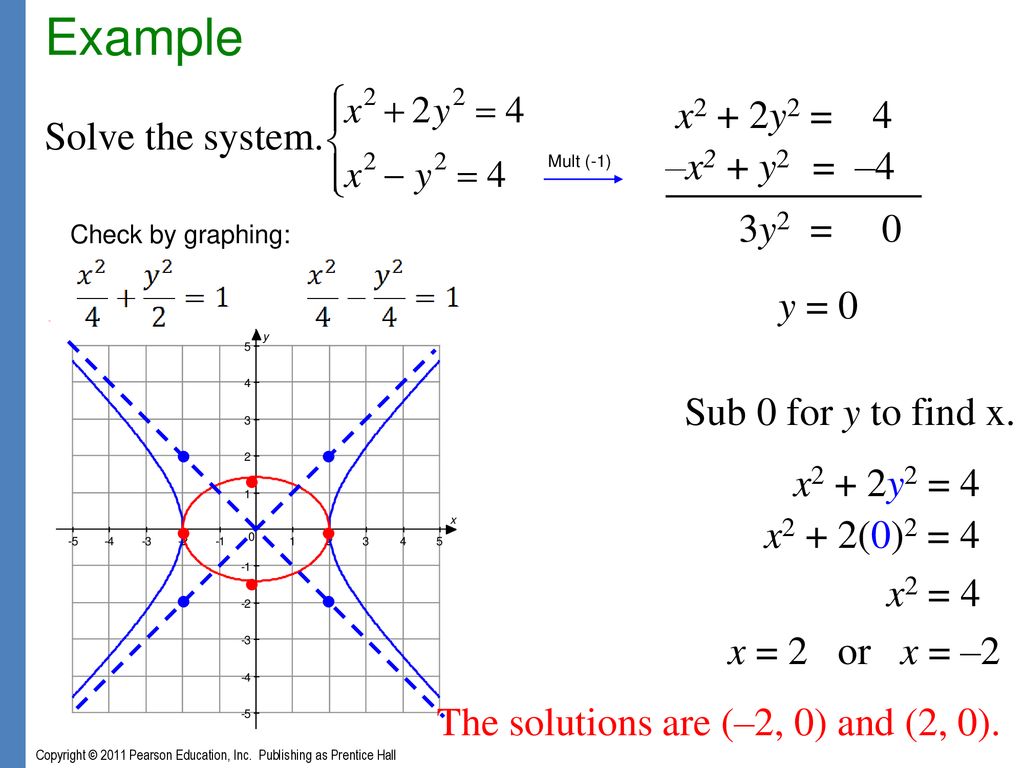



Graphing Quadratic Functions Rational Functions Conic Sections Ppt Download
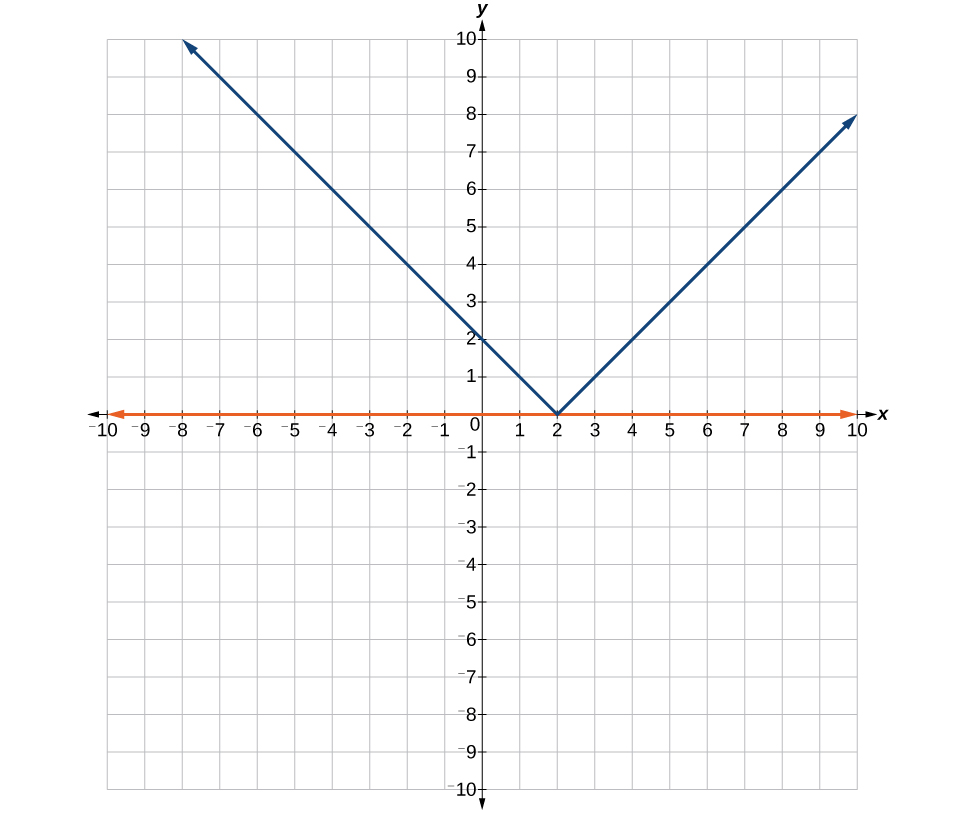



Solutions College Algebra



2




Tutto 1 Di 2 Flashcards Quizlet




Solve X 2 5x 6 0 Youtube



H 2 0 High Resolution Stock Photography And Images Page 15 Alamy



Inverse Function




Pdf A Nonlinear Model Of The Unsteady Heat Transfer Through An Electron Tube



1



0 件のコメント:
コメントを投稿